Time Series Lecture
In this chapter, we begin to study the properties of the Ordinary Least Squares (OLS) for estimating linear regression models using time series data. In section 1.0 we discuss some conceptual differences between time series and cross-sectional data. The next section will explore some samples of time series regressions that are often estimated in the empirical social studies. This is then followed by an examination of the finite sample properties of the OLS estimators and the Gauss Markov assumptions and classical linear model assumptions for time series regression. Moving on, this chapter will look at the principles of serial correlation and autocorrelation. In dealing with autocorrelation, we will study first-order correlation and higher-order autocorrelation.
In addition, we return to some of the basic concepts and definitions regarding univariate time series. This will touch on the stationarity concept (making the critical distinction between stationary and nonstationary time-series processes) and the autocorrelation function and the moving average process. Moreover, the Box Jenkins approach for modelling ARMA will be introduced in this chapter. In the penultimate chapter, we will explore the error correction model to test for cointegration, this time introducing Unit root testing and the Engle-Granger method. The final chapter will cover simple panel data methods.
1. What is time series data
A significant number of the properties and standards explored in cross-section econometrics proceed when our data are gathered over time. A time series is an ordered grouping of numerical data points/observations on a variable that are taken at discreet and similarly spaced time intervals. We list the time periods as 1,2, …, T and symbolise the set of variables as (y1, y2,….yT). The key here is that the data points must be in progressive order. In other words, temporal ordering is an undeniable trademark that differentiates time series data from cross-sectional data. In the social sciences, when analysing time series data, we must acknowledge that the past can impact the future, however not the other way round. To highlight the appropriate ordering of time series data, table 2.1, gives a partial listing of the data on UK inflation and unemployment rates.
Table 1.0 Partial listing of data on UK inflation and unemployment rates, 1956-2003
|
Year |
Inflation |
Unemployment |
|
1956 |
3.04 |
1.3 |
|
1957 |
4.64 |
1.6 |
|
1958 |
1.85 |
2.2 |
|
1959 |
0 |
2.3 |
|
. |
. |
. |
|
. |
. |
. |
|
. |
. |
. |
|
1998 |
1.55 |
6.25 |
|
1999 |
1.2 |
5.975 |
|
2000 |
0.75 |
5.4 |
|
2001 |
1.07 |
5.1 |
|
2002 |
1.69 |
5.2 |
|
2003 |
1.25 |
5 |
|
. |
. |
. |
|
. |
. |
. |
Source: Historical inflation rates have been collected from inflation.eu (http://www.inflation.eu/inflation-rates/great-britain/historic-inflation/cpi-inflation-great-britain.aspx) , whilst the unemployment data up to 1959 has been collected from an ONS historical unemployment special feature (http://webarchive.nationalarchives.gov.uk/20160106165440/http://www.ons.gov.uk/ons/dcp171778_374770.pdf) the rest has been gathered (1998 - 2003) from indexmundi (https://www.indexmundi.com/united_kingdom/unemployment_rate.html )
Need Help With Your Economics Essay?
If you need assistance with writing a economics essay, our professional essay writing service can provide valuable assistance.
See how our Essay Writing Service can help today!
The usage of time series models is bifold. They are used to:
- Fit a model and advance to forecasting, monitoring or even feedback and feedforward control.
- Obtain a comprehension of the basic powers and structure that produced the observed data
Time series analysis is used for many applications including
- Budgetary analysis
- Stock market analysis
- Economic forecasting
- Yield projections
- Census analysis
- And more…
Lastly, time-series data exhibit imperative difficulties that are absent with cross section data and that warrant detailed attention. With cross sectional data, the OLS estimates computed from various random samples will by and large vary (hence why the OLS estimators are considered to be random). The difference with time series data is more inconspicuous: economic time series data fulfils the natural requirements for being outcomes of random variables. For instance, today we do not know what the NASDAQ Composite or S&P 500 will be at the close of the next trading day. We do not know what the annual growth rate in output will be in Germany during the coming year. Since these outcomes are clearly unknown, they should be viewed as random variables. Formally, a grouping of variables by time is called a stochastic process/time series process.
1.1 Examples of time series regression models.
1.1.1 static models
yᵼ = β₀ + β₁Xᵼ + uᵼ, t = 1, 2, . . . , T
Where T is the number of observation in the time series. The relation between y and x is contemporaneous.
Usually, a static model is postulated when a change in x at time t is believed to have an immediate effect on y: 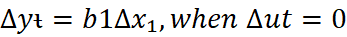
Example: Static Phillips Curve:
inflationt = β₀ + β₁unemploymentᵼ + uᵼ
This type of the Philips curve assumes a constant natural rate of employment and constant inflationary expectations, and it can be utilised to contemplate the contemporaneous trade-off between inflation and unemployment.
Naturally, we can have several independent variables in a static regression model. Let altrte denote the assaults per 50, 000 people in Nottingham, England during year t, let convrte denote the assault conviction rate, let pvrty be the local poverty rate, drgadd be the level of drug addiction in Nottingham and yndmale be the fraction of the population consisting of males between the ages of 16 and 25. Then a static multiple regression model explaining assault rates is:
Altrteᵼ = β₀+ β₁convrte+ β₂pvrty+ β₃drgadd+ β₄yndmale+Uᵼ
Utilising a model such as this, we can hope to evaluate for example, the ceteris paribus effect of an expansion in the conviction rate on a specific criminal activity
1.1.2 Finite Distributed Lag (FDL) models
In FDL models, earlier values of one or more explanatory variables affect the current value
of y.
(2) yᵼ = α₀ + δ₀xᵼ + δ₁xᵼ-₁+ δ₂xᵼ-₂ + uᵼ
is an FDL of order two.
Multipliers
Multipliers indicate the impact of a unit change in x on y.
Impact Multiplier: Indicates the immediate one unit change in x on y. In (2) δ0 is the impact multiplier.
To see this, suppose xᵼ is constant, say c, before time point t, increases by one unit to
c + 1 at time point t and returns back to c at t + 1. That is
· · · , xᵼ₋₂ = c, x₋₁= c, xᵼ = c + 1, xᵼ+₁= c, xᵼ+₂= c, . . .
Suppose for the sake of simplicity that the error term is zero, then
yᵼ₋₁ = α₀ + δ₀c + δ₁c + δ₂c
yᵼ = α₀ + δ₀(c + 1) + δ₁c + δ₂c
yᵼ+₁ = α₀ + δ₀c + δ₁(c + 1) + δ₂c
y ᵼ+₂ = α₀ + δ₀c + δ₁c + δ₂(c + 1)
y ᵼ+₃ = α₀ + δ₀c + δ₁c + δ₂c
from which we find
yᵼ − yᵼ₋₁ = δ₀,
which is the immediate change in yᵼ.
In the next period, t + 1, the change is
yᵼ+₁ − yᵼ₋₁= δ₁,
after that
yᵼ+₂ − yᵼ₋₁ = δ₂,
after which the series comes back to its underlying
level yᵼ+₃ = yᵼ₋₁. The series {δ₀, δ₁, δ₂} is called the lag distribution, which abridges the dynamic effect that an impermanant increase in x has on y
Lag Distribution: A graph of δj as a function of j summarizes the distribution of the
effects of a one unit change in x on y as a function of j, j = 0, 1, . . ..
Especially, if we standardize the initial value of y at yt−1 = 0, the lag distribution follows out the consequent estimates of y due to a one unit, temporary change in x.
Interim multiplier of order J:
(3) δ(J) = 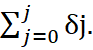
Indicates the cumulative effect up to J of a unit change in x on y.
In (2) e.g., δ(1) = δ₀ + δ₁.
Total Multiplier: (Long-Run Multiplier)
Indicates the total (long-run) change in y as a response of a unit change in x.
(4) 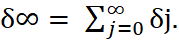
Later on, we will be look at the class of models called ARIMA models (Autoregressive Integrated Moving Average). Before we do, we will examine the finite sample properties of OLS under Classical assumptions.
2. Finite sample properties of OLS under classical assumptions
Issues in using OLS with time series data.
2.1 Unbiasedness of OLS
2.1.1 The time series/stochastic process ought to take after a model that is linear in its parameters
This assumption is essentially the same as the cross-sectional supposition, except we are now indicating a linear model for time series data.
The stochastic process is a gathering of random variables {Xt} indexed by a set T, i.e. t ∈ T. (Not necessarily independent!)
{(Xᵼ₁,Xᵼ₂,…….Xᵼᴋ, yᵼ) : t = 1,2,….n} follows the linear model:
yᵼ = β₀ + β₁xᵼ₁ +………, BᴋXᵼᴋ + uᵼ
2.1.2 No perfect collinearity
In the sample and along these lines in the fundamental time series process, no independent variable is constant nor a perfect linear combination of the others.
2.1.3 Zero conditional mean
For each t, the expected value of the error Uᵼ, given the explanatory variables for all time periods, is zero. Mathematically,
E(Uᵼ|X) = 0, t = 1,2,….n.
This presumption suggests that the error term Uᵼ, is uncorrelated with each independent variable in every time period. The way this is expressed as far as the conditional expectation implies that we likewise accurately determine the functional relationship between Yᵼ and the independent variable.
We need to add two assumptions to round out the Gauss-Markov assumptions for time series regressions: Homoskedasticity (which is mentioned in cross-sectional analysis) and No serial correlation.
2.1.4 Homoskedasticity
Conditional on X, the variance of uᵼ, is the same for all t: Var(Uᵼ|X) = Var(uᵼ) =
This assumption means that (Var(UᵼX) cannot depend on X- it is sufficient that Uᵼ and X are independent-and that (Var(Uᵼ) must be constant over time.
2.1.5 Serial correlation
Serial correlation is a problem associated with time-series data. It occurs when the errors of the regression model are correlated with their own past values. Serial correlation by itself does not mean that OLS will be biased. The most common effect of serial correlation is to bias downwards the standard errors of the OLS estimator (though this is not always the case).
The disturbance term relating to any observation is influenced by the disturbance term relating to any other observation Since this is not consistent with the Gauss-Markov assumption of serially independent errors, it follows that OLS is no longer BLUE.
2.2 Serial correlation and autocorrelation
As mentioned above, serial correlation is a general term used to describe any situation in which the error terms are not completely independent. Autocorrelation is a particular type of serial correlation in which the error terms are a function of their own past values.
ᴜ₊ = pᴜᴌ₋₁ + eᴌ The first equation is known as an AR (1)
ᴜ₊ = e₊ + ae₊₋₁ The second equation is known as a MA (1)
Both of these equations describe serial correlation but only the first describes autocorrelation. The second equation describes a moving average error which is a different type of serial correlation.
Need Help With Your Economics Essay?
If you need assistance with writing a economics essay, our professional essay writing service can provide valuable assistance.
See how our Essay Writing Service can help today!
2.2.1 First-order autocorrelation
Many forms of autocorrelation exist. The most popular one is first-order autocorrelation.
Consider
Yt = βXt + ut
ut = ρut₋₁ + et as we know called an AR(1)
where the error term depends upon his predecessor or the current observation of the error term ut is a function of the previous (lagged) observation of the error term:
εt is an error with mean zero and constant variance. Assumptions are such that the Gauss-Markov conditions arise if ρ = 0.
- The coefficient ρ (RHO) is called the autocorrelation coefficient and takes values from -1 to +1.
- The size of ρ will determine the strength of the autocorrelation.
- There can be three different cases:
- If ρ is zero, then we have no autocorrelation.
- If ρ approaches unity, the value of the previous observation of the error becomes more important in determining the value of the current error and therefore high degree of autocorrelation exists. In this case we have positive autocorrelation.
- If ρ approaches -1, we have high degree of negative autocorrelation.
Properties of ut
To determine the properties of ut, we assume | ρ | < 1 stationarity condition)
Then it holds that:
E(ut ) = ρE(u₊₋₁ )+ E(εt ) = 0 (1)
var(ut ) = E(u ) = ρs
) = ρs 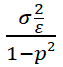 (2)
(2)
cov(ut ,ut+s ) = E(ut ,ut-s )= ρs 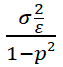 (3)
(3)
cor(ut ,uᴌ+s ) = ρs (4)
(note that this requires -1 < ρ < 1.)
2.2.2 Higher-order Autocorrelation
Second order when:
ut=ρ1ut-1+ ρ2ut-2+et
Third order when:
ut=ρ1ut-1+ ρ2ut-2+ρ3ut-3 +et
p-th order when:
ut=ρ1ut-1+ ρ2ut-2+ρ3ut-3 +…+ ρput-p +et
3. ARMA model using the Box and Jenkins approach
Time series modelling is used to analyse and find properties of economic time series under the idea that ‘the data speaks for itself’. Time series models allows 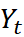 to be explained by the past or lagged values of
to be explained by the past or lagged values of  itself (the AR component) and current and lagged values of (the MA component), which is an uncorrelated random error term with zero mean and constant variance - that is, a white noise error term.
itself (the AR component) and current and lagged values of (the MA component), which is an uncorrelated random error term with zero mean and constant variance - that is, a white noise error term.
Building the ARMA model follows 3 stages as approached by Box and Jenkins. These are identification, estimation and diagnostic checking.
3.1 Model Identification
First, an ARMA model can only be identified for stationary series. If the variables employed are non-stationary, then it can be proved that the standard assumptions for asymptotic analysis will not be valid. In other words, the t-ratios will not follow a t distribution, and the f-statistic will not follow an f-distribution. Standard t ratios can take enormously large value, making hypothesis tests invalid. A time series plot is used as an informal test for stationarity. The series is considered stationary if the level and the spread do not exhibit any visual changes over time.
The formal test is done by testing for a unit root using Augmented Dickey Fuller (ADF) model. Augments the Dickey Fuller using ƿ lags of the dependent variable. The lags of Δу₊ soaks up any dynamic structure present in the dependent variable, to ensure that υ₊ is auto correlated. An information criterion is used to determine the optimal lag length by choosing number of lags that minimises its value.
If the û₊ is 1(1) then the model would employ specifications in first differences only.
The ACF and the PACF of the stochastic process (real exchange rate) are observed to see if it decays rapidly to zero. ARMA process will have a geometrically declining ACF and PACF. As a helping tool to test for significance of a correlation coefficient, it can be tested if is outside this band:
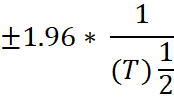
3.2 Model Estimation
Using ADF and observing ACF and PACF do not clear whether or not the variance of the differenced series is time invariant. In this case, information criteria is used for model selection.
This report uses Akaike’s information criterion (AIC), and the Schwarz’s Bayesian information criterion (SBIC).
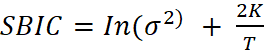 and
and 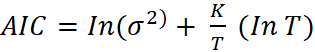
However, this method is not benign since it affects the relative strength of the penalty term compared with the error variance (Brooks 2014). In Eviews, this can be done by estimating each of the models (p,q) order using least squares and noting the SBIC and AIC in each case and pick the minimum values.
3.3 Model Diagnostics
This is done through:
I. Residual diagnostics - the pattern of white noise residual of the model fit will be assessor by plotting the ACF and the PACF or we perform Ljung Box Test on the residuals.
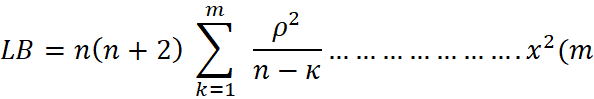
H₀ = no serial correlation
H₁ = there is serial correlation
Where m = lag length, n is the sample size and is ρ the sample autocorrelation coefficient
A critical restriction of Box-Jenkins is the requirement for human inference, for example understanding of ACF’s and PACF’s. This gives way to confusion and misconceptions, and may limit meaningful comparison between diverse data sets and models.
3.4 Forecasting
After every one of the steps are finished, meta-diagnosis on the model fit will help know forecasting, and reliability which will be the judge through use the use of the smallest mean square error, mean absolute error (MAE), mean absolute percentage error (MAPE), root mean square error (RMSE) and mean square error (MSE). Note, models making use of weekly (or lower frequency) data do not enable one to quantifiably measure how markets respond to some information, for example, an adjustment to the interest rates, because the change has already occurred and the information has been consumed by the time you predict it (Weisang and Awazu, 2008).
4. Cointegration
This section will explore how to test for cointegration beginning with an examination of how to test the residuals for a unit root (ADF test) all the way to estimating the error correction model (ECM). Economic theory often suggests that certain parts of financial or economic variables should be linked by a long-run economic relationship. If we have two non-stationary time series X and Y that become stationary when differenced (these are called integrated of order one series, or I(1) series; random walks are one example) such that some linear combination of X and Y is stationary (aka, I(0)), then we say that X and Y are cointegrated.
Some examples include:
- Growth theory models imply cointegration between income, consumption and investment.
- The permanent income hypothesis implies cointegration between consumption and income.
- Purchasing power parity (PPP) implies cointegration between the nominal exchange rate and domestic and foreign prices.
- The movement of world commodity prices compared against domestic prices
4.1 Testing for a unit root
Hypothesis - given the sample of data to hand, is it plausible that the true data generating process for y contains one or more unit roots?
Augmented Dickey Fuller (ADF) model with no intercept and trend
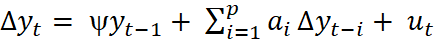
The Augmented Dickey Fuller expands on the Dickey Fuller test using ƿ lags of the dependent variable. The lags of Δу₊ soaks up any dynamic structure present in the dependent variable, to ensure that υ₊ is not auto correlated (Brooks 2014). For determining the optimal number of lags, the two simple rules of thumb are usually suggested. To begin with, the frequency of data can be used to decide (i.e. if data is monthly = 12 lags; if quarterly = 4 lags). Second, an information criterion can be utilised to choose by picking the number of lags that minimises its value mainly Schwarz information criterion (SIC) and the Akaike information criterion (AIC). After making sure the series are stationary after first difference (note regression amid this stage will give spurious results), the following stage is to use the Engle-Granger 2 step method.
4.2 Engle-Granger
Assume the Engle and Granger combination that defines the dynamic long-run equilibrium relationship between the price in a domestic market P₁ and the price in world market P₂:
P¹₊ = α₀ + α₁P²₊ + µ₊
Where µ₊ is a random error with constant variance that can be simultaneously correlated. Dwyer and Wallace (1992) express that long-run market integration test within this structure series whether any stable long-run relationship exists between the two price series. While, Alexander and Wyeth (1994) state that short run market integration tests expect to find out whether prices in different markets react promptly to the long run relationship said above. No cointegration suggests that series could wander apart without bound in the long run.
The Process
This involves running a static regression;
yt = θ’xt + et ,
The asymptotic distribution θ is not standard but the test suggested was to estimate θ by OLS.
Step 1
Subsequent to making sure that all variables are 1(1), step 1 of Engle-Granger requires estimating the cointegration regression using OLS. Then save the residuals of the cointegrating regression û₊.
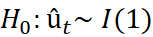
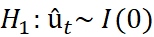
The essential goal is to inspect the null hypothesis that there is a unit root in the potentially cointegrating regression residuals, while under the alternative, the residuals are stationary. Under the null hypothesis, therefore a stationary linear combination of the non-stationary variables has not been found. Hence, if the null hypothesis is not rejected, there is no cointegration. For this situation, the model would utilise specifications in first differences only. On the other hand, if the null of a unit root in the potential cointegrating regression’s residual is rejected, it would be presumed that a stationary linear combination of the non-stationary has been found. Along these lines, the variables would be classed as cointegrated. The fitting technique would be to form and estimate an error correction model (Brooks 2014). If the residuals are 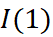 , the model would need to be estimated containing only first differences showing the short run solution written as
, the model would need to be estimated containing only first differences showing the short run solution written as 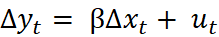
Step 2
Estimate the error correction model using residuals rom the first step as one variable
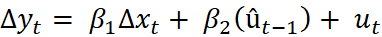
Where 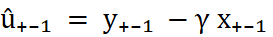
The standard notation form:
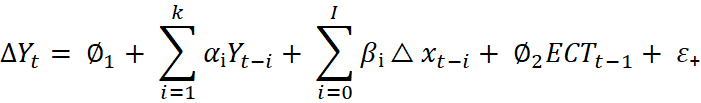
Where ECT is the Error Correction term (û₊₋₁ = Y₊₋₁ - α₀ - α₁X₊₋₁)
Rejection of the null hypothesis of no cointegration shows that the residuals are stationary with mean zero.
Advantages of ECM
- It is a helpful model measuring the correction from a deviation from equilibrium, making it a phenomenal economic application.
- It wipes out the issue of spurious regressions when the cointegrated ECMs are detailed in terms of 1st differences.
- Disequilibrium error term is a stationary variable. Thusly, ECM has essential ramifications: the way that the two variables are cointegrated suggests there is some adjustment process which prevents errors in the long-run relationship from getting to be noticeably bigger and bigger.
Limitations
- The causality Problem - The issue of simultaneous equation bias - that is the point at which the causality between y and x runs in both directions, but the Engle-Granger method requires normalisation on one variable and this can be tended to by the Johansen approach.
- Both unit root and cointegration tests have low power in finite samples. However, this is a small sample problem that ought to vanish asymptotically.
- We cannot perform any hypothesis tests about the actual cointegrating relationship estimated at first stage. This can be tended to by the Engle and Yoo approach.
4.3 Granger Causality test
Granger (1969), alluded to tests that try to seek answers to a question such as ‘Do changes in p1 cause changes in p2’? Time series p1 is said to Granger-cause p2 if it can be demonstrated that lags of y1 values provide statistically significant information about future value of p2.
- The t-test shows that the lagged value is significant and;
- The f-test show that the lagged value and all the other lagged values are jointly significant in explaining future values of the other variable.
The null hypothesis of no Granger causality cannot be rejected if no lagged values of the explanatory variable are retained in the regression. If both sets of lags are significant, there is bi-directional causality. It is likewise conceivable that neither set of lags will be statistically significant in the equation for the other variable, in other words both series are independent of each other.
5. Simple panel data methods
The next section moves on to the coverage of multiple regression using pure time series data or pure cross-sectional data. There are two types of data that have both cross-sectional and time dimensions: independently pooled cross sections (IPCS) and panel, or longitudinal data.
5.1 Independent pooling
Consider a situation where 4,000 likely voters are sampled each week by YouGov to determine their fulfilment with the Brexit talks, and we have 20 weeks of those survey data. We have 80,000 observations, each identified by a respondent code and the date on which it was gathered. In spite of the fact that the respondent codes keep running from 1 to 4,000 every week, we take note that Mr. 2,464 this week has no connection to Mr. 2,464 next week or the week after. These are independent surveys, each representing a random sample from the population, which rules out correlation in the error terms within each survey’s observations. Only by chance will a similar individual appear more than once in the pooled dataset, and regardless of the possibility that she does, won’t know it. Subsequently, we have 20 independent cross sections and may pool them into.
Surveys, for example, the Annual Population Survey (APS) represents independently pooled cross section (IPCS) data, as in that a random sample of UK households is drawn at each time period. There are no connections between households showing in the sample in 2016 and those appearing in 2017.
5.2 The advantages of pooling
We gain sample size, of course, which will surge the exactness of estimators if the links being assessed are transiently steady. With that proviso, we can utilise IPCS to draw conclusions about the populace at more than a single point in time, and make deductions about how UK households acted amid for example, the 1990s as opposed to simply in 1995. Temporal stability of any relationship may not be sensible, so we frequently take into consideration some variety across time periods: most commonly, in the intercept term of the relationship for each time period, which can readily be accomplished with indicator variables.
5.3 Panel data methods
A panel data set, while having both a cross sectional and time series dimension contrasts in some essential regards from an independently pooled cross section (which is acquired by sampling randomly from a large population at different points in time). To gather panel data - which is sometimes called longitudinal data - we take after or endeavour to take after some individuals, states, families, cities or whatever, across time. For instance, a panel data set on individual wages, hours, education and other factors is gathered by randomly selecting people from a population at a given point in time. Then, these same people are re-interviewed at several subsequent points in time. This gives us data on wages, hours, education et cetera, for the same group of people in various years.
5.3.1 Panel data brief description
Each of N individual’s data is measured on T occasions
- Individuals may be people, firms, countries etc
- Some variables change over time for t = 1,…,T
- Some variables may be fixed over the time period, such as gender, the geographic location of a firm or a person’s ethnic group
- When there are no missing data, so that there are NT observations, then we have a balanced panel (less than NT is called an unbalanced panel)
- Typically, N is large relative to T, but not always
With observations that span both time and individuals in a cross-section, more information is available, giving more efficient estimates.
- The use of panel data allows empirical tests of a wide range of hypotheses.
- With panel data we can control for:
- Unobserved or unmeasurable sources of individual heterogeneity that vary across individuals but do not vary over time
- omitted variable bias
5.4 Two-period panel data analysis
In its most straightforward frame, panel data alludes to estimations of yᵢ,ᵼ, t = 1, 2: two cross-sections on the same units, i = 1, . . . , N. Say that we run a regression on one of the cross-sections. Any regression may well show the ill effects of omitted variables bias: there are various elements that may impact the cross-sectional result, past the involved regressors. One method would be to attempt to capture as many of those components as would be prudent by measuring them and incorporating them in the analysis. For example, a city-level examination of crime rates versus the city’s level of unemployment may be enlarged with control factors such as age dispersion, city size, gender distribution and, education levels, ethnic makeup, recorder wrongdoing rates et cetera.
An alternative method would study huge numbers of these city-particular factors as unobserved heterogeneity, and use panel data from rehashed estimates on the same city to capture their net impacts. Some of those facets are time invariant (or roughly so), while some city specific components will change after some time. We can manage the greater part of the time-invariant components on the off chance we have no less than two estimations for every city by considering them as individual fixed effects. In like manner, the net impact of all time-varying factors can be managed by a time fixed effect. For a model (such as suicide rate vs. unemployment rate) with a solitary explanatory variable, yᵢᵼ = β₀ + γ₀d2ᵼ + β1Xᵢᵼ + aᵢ + uᵢᵼ (5) where the indicator variable d2ᵼ is zero for period one and one for period two, not varying over i. Both the y variable and the X variable have both i and t subscripts, varying across (e.g.) cities and the two time periods, as does the error term u. For the suicide rate example, coefficient γ₀ picks up a macro effect: for example, suicide rates across the UK may have varied, on average, between the two time periods. The individual time effect picks that up. The term aᵢ is an individual fixed effect, with a different value for each unit (city) but not varying over time. It grabs the effect of everything beyond X that makes a specific city one-of-a-kind, without our specifying what those components might be. By what method might we estimate equation (5)? On the off chance that we just pool the two years’ data and run OLS, we can infer estimates of the β and γ parameters, however we are overlooking the ai term, which is being incorporated in the factor error term vᵢᵼ = aᵢ + uᵢᵼ. Unless we can be sure that E(vᵢᵼ|Xᵢᵼ) = 0, the pooled method will prompt biased and inconsistent estimates. This zero conditional mean supposition expresses that the unobserved city-specific heterogeneity must not be correlated with the X variable: in the example, with the unemployment rate.
But if a city customarily has endured high unemployment and a deficiency of steady employment, it might likewise have historically high crime rates. This will infer that this correlation is very likely to be nonzero, and OLS will be biased. This same contention applies if we use a single cross section; as we depicted above, we would be likely to disregard various critical quantifiable factors in estimating the simple regression from a cross-section of cities at one point in time.
References
Alexander, Carol, and John Wyeth. 1994. Cointegration and market integration: an application to the Indonesian rice market. Journal of Development Studies 30: 303-328.
Brooks, Chris. 2014. Introductory econometrics for finance. 3d ed. Cambridge: Cambridge University Press.
Dwyer, Gerald P., and Myles S. Wallace. 1992. Cointegration and market efficiency. Journal of International Money and Finance 11: 318-327.
Granger, Chris W.J. 1969. Investigating causal relations by econometric models and cross-spectral methods. Econometrica 37: 424-438.
Weisang, G., and Awazu, Y., 2008. Vagaries of the Euro: An Introduction to ARIMA Modelling. Article in Journal [online]. 2 (1) pp.45-55. Available via: Econbiz
Cite This Module
To export a reference to this article please select a referencing style below:
 GBR
GBR 







